Workarounds to include R stat functions in data science pipelines
This post explores some of the possible workarounds that can be employed
if you want to include non-pipe-aware functions to magrittr pipelines
without using intubate and, at the end, the intubate alternative. See
intubate <||> R stat functions in data science pipelines for an introduction.
Some workarounds to include non-pipe-aware functions in pipelines.
library(magrittr)
Example 1:
Using lm directly in a data pipeline will raise an error
LifeCycleSavings %>%
lm(sr ~ .)
## Error in as.data.frame.default(data): cannot coerce class ""formula"" to a data.frame
lm can be added directly to the pipeline,
without error, by specifying the name of the parameter
associated with the model (formula in this case).
LifeCycleSavings %>%
lm(formula = sr ~ .)
##
## Call:
## lm(formula = sr ~ ., data = .)
##
## Coefficients:
## (Intercept) pop15 pop75 dpi ddpi
## 28.5660865 -0.4611931 -1.6914977 -0.0003369 0.4096949
The drawback of this approach is that not all functions
use formula to specify the model.
So far I have encountered 5 variants:
formulaxobjectmodel, andfixed
The following are examples of functions using the other variants.
Example 2:
Using xyplot directly in a data pipeline will raise an error
library(lattice)
iris %>%
xyplot(Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
## Error in UseMethod("xyplot"): no applicable method for 'xyplot' applied to an object of class "data.frame"
unless x is specified.
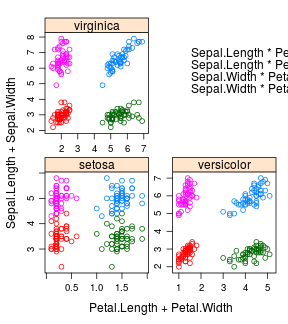
iris %>%
xyplot(x = Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
Example 3:
Using tmd (a different function in the same package)
directly in a data pipeline will raise an error
library(lattice)
iris %>%
tmd(Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
## Error in UseMethod("tmd"): no applicable method for 'tmd' applied to an object of class "data.frame"
unless object is specified.
iris %>%
tmd(object = Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
Example 4:
Using gls directly in a data pipeline
will raise an error
library(nlme)
Ovary %>%
gls(follicles ~ sin(2*pi*Time) + cos(2*pi*Time),
correlation = corAR1(form = ~ 1 | Mare))
## Error in gls(., follicles ~ sin(2 * pi * Time) + cos(2 * pi * Time), correlation = corAR1(form = ~1 | :
## model must be a formula of the form "resp ~ pred"
unless model is specified.
Ovary %>%
gls(model = follicles ~ sin(2*pi*Time) + cos(2*pi*Time),
correlation = corAR1(form = ~ 1 | Mare))
## Generalized least squares fit by REML
## Model: follicles ~ sin(2 * pi * Time) + cos(2 * pi * Time)
## Data: .
## Log-restricted-likelihood: -780.7273
##
## Coefficients:
## (Intercept) sin(2 * pi * Time) cos(2 * pi * Time)
## 12.2163982 -2.7747122 -0.8996047
##
## Correlation Structure: AR(1)
## Formula: ~1 | Mare
## Parameter estimate(s):
## Phi
## 0.7532079
## Degrees of freedom: 308 total; 305 residual
## Residual standard error: 4.616172
Example 5:
Using lme directly in a data pipeline
will raise an error
library(nlme)
Orthodont %>%
lme(distance ~ age)
## Error in (function (fixed, data = sys.frame(sys.parent()), random, correlation = NULL, : formal argument "data" matched by multiple actual arguments
unless fixed(!) is specified.
Orthodont %>%
lme(fixed = distance ~ age)
## Linear mixed-effects model fit by REML
## Data: .
## Log-restricted-likelihood: -221.3183
## Fixed: distance ~ age
## (Intercept) age
## 16.7611111 0.6601852
##
## Random effects:
## Formula: ~age | Subject
## Structure: General positive-definite
## StdDev Corr
## (Intercept) 2.3270339 (Intr)
## age 0.2264276 -0.609
## Residual 1.3100399
##
## Number of Observations: 108
## Number of Groups: 27
Having to remember the name of the parameter associated to the model in each case is inconvenient, may be error prone, and gives an inconsistent look and feel to an otherwise elegant interface.
Moreover, it is consider good practice in R to not specify the name of the first two parameters (and in pipes the first is implicit), and name the remaining.
Not having to specify the name of the model argument completely hides the heterogeneity of names that can be associated with it. You only write the model and completely forget which name has been assigned to it.
More complicated workarounds
There are functions that rely on the order of the parameters
(such as aggregate, cor.test and other 28 I found so far) that will still
raise an error even if you name the model.
In fact, there are cases where it is not true that if in a function call you name the parameters you can write them in any order you want.
One example is cor.test:
1) Unnamed parameters in the natural order. Works
cor.test(~ CONT + INTG, USJudgeRatings)
##
## Pearson's product-moment correlation
##
## data: CONT and INTG
## t = -0.8605, df = 41, p-value = 0.3945
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4168591 0.1741182
## sample estimates:
## cor
## -0.1331909
2) Named parameters in the natural order. Works
cor.test(formula = ~ CONT + INTG, data = USJudgeRatings)
##
## Pearson's product-moment correlation
##
## data: CONT and INTG
## t = -0.8605, df = 41, p-value = 0.3945
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4168591 0.1741182
## sample estimates:
## cor
## -0.1331909
3) Named parameters with the order changed. Doesn’t work!
cor.test(data = USJudgeRatings, formula = ~ CONT + INTG)
## Error in cor.test.default(data = USJudgeRatings, formula = ~CONT + INTG): argument "x" is missing, with no default
Let’s see what happens if we want to add these cases to the %>% pipeline.
Example of error 1: cor.test
Using cor.test directly in a data pipeline will raise an error
USJudgeRatings %>%
cor.test(~ CONT + INTG)
## Error in cor.test.default(., ~CONT + INTG): 'x' and 'y' must have the same length
even when specifying formula (as it should be according to
the documentation).
USJudgeRatings %>%
cor.test(formula = ~ CONT + INTG)
## Error in cor.test.default(., formula = ~CONT + INTG): argument "y" is missing, with no default
Was it y then?
USJudgeRatings %>%
cor.test(y = ~ CONT + INTG)
## Error in cor.test.default(., y = ~CONT + INTG): 'x' and 'y' must have the same length
No…
Was it x then?
USJudgeRatings %>%
cor.test(x = ~ CONT + INTG)
## Error in cor.test.formula(., x = ~CONT + INTG): 'formula' missing or invalid
No
Example of error 2: aggregate
Using aggregate directly in a data pipeline
will raise an error
ToothGrowth %>%
aggregate(len ~ ., mean)
## Error in aggregate.data.frame(., len ~ ., mean): 'by' must be a list
even when specifying formula
ToothGrowth %>%
aggregate(formula=len ~ ., mean)
## Error in match.fun(FUN): argument "FUN" is missing, with no default
or other variants.
Example of error 3: lda
Using lda directly in a data pipeline
will raise an error
library(MASS)
Iris <- data.frame(rbind(iris3[,,1], iris3[,,2], iris3[,,3]),
Sp = rep(c("s","c","v"), rep(50,3)))
Iris %>%
lda(Sp ~ .)
## Error in lda.default(x, grouping, ...): nrow(x) and length(grouping) are different
even when specifying formula.
Iris %>%
lda(formula = Sp ~ .)
## Error in lda.default(x, grouping, ...): argument "grouping" is missing, with no default
or other variants.
Let’s try another strategy. Let’s see if the %$% operator, that expands the names of the variables inside the data structure, can be of help.
Iris %$%
lda(Sp ~ .)
## Error in terms.formula(formula, data = data): '.' in formula and no 'data' argument
Still no…
One last try…
Iris %$%
lda(Sp ~ Sepal.L. + Sepal.W. + Petal.L. + Petal.W.)
## Call:
## lda(Sp ~ Sepal.L. + Sepal.W. + Petal.L. + Petal.W.)
##
## Prior probabilities of groups:
## c s v
## 0.3333333 0.3333333 0.3333333
##
## Group means:
## Sepal.L. Sepal.W. Petal.L. Petal.W.
## c 5.936 2.770 4.260 1.326
## s 5.006 3.428 1.462 0.246
## v 6.588 2.974 5.552 2.026
##
## Coefficients of linear discriminants:
## LD1 LD2
## Sepal.L. -0.8293776 0.02410215
## Sepal.W. -1.5344731 2.16452123
## Petal.L. 2.2012117 -0.93192121
## Petal.W. 2.8104603 2.83918785
##
## Proportion of trace:
## LD1 LD2
## 0.9912 0.0088
Finally! But… we had to specify all the variables
(and they may be a lot), and use %$% instead of %>%.
There is still another workaround that allows
these functions to be used directly in a pipeline.
It requires the use of another function (with)
encapsulating the offending function. Here it goes:
Iris %>%
with(lda(Sp ~ ., .))
## Call:
## lda(Sp ~ ., data = .)
##
## Prior probabilities of groups:
## c s v
## 0.3333333 0.3333333 0.3333333
##
## Group means:
## Sepal.L. Sepal.W. Petal.L. Petal.W.
## c 5.936 2.770 4.260 1.326
## s 5.006 3.428 1.462 0.246
## v 6.588 2.974 5.552 2.026
##
## Coefficients of linear discriminants:
## LD1 LD2
## Sepal.L. -0.8293776 0.02410215
## Sepal.W. -1.5344731 2.16452123
## Petal.L. 2.2012117 -0.93192121
## Petal.W. 2.8104603 2.83918785
##
## Proportion of trace:
## LD1 LD2
## 0.9912 0.0088
In the case of aggregate it goes like
ToothGrowth %>%
with(aggregate(len ~ ., ., mean))
## supp dose len
## 1 OJ 0.5 13.23
## 2 VC 0.5 7.98
## 3 OJ 1.0 22.70
## 4 VC 1.0 16.77
## 5 OJ 2.0 26.06
## 6 VC 2.0 26.14
In addition, there is the added complexity of
interpreting the meaning of each of those .
(unfortunately they do not mean the same)
which may cause confusion, particularly at a future
time when you may have to remember why you had to
do this to yourself… (the first is specifying to include in the
rhs of the model all the variables in the data but len,
the second is the name of the data
structure passed by the pipe. Yes, it is called .!)
It is also a solution for the case of cor.test before,
(and it should work in any case):
USJudgeRatings %>%
with(cor.test(~ CONT + INTG, .))
##
## Pearson's product-moment correlation
##
## data: CONT and INTG
## t = -0.8605, df = 41, p-value = 0.3945
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4168591 0.1741182
## sample estimates:
## cor
## -0.1331909
Undoubtedly, there may be more elegant workarounds that I am unaware of. But the point is that, no matter how elegant, they will be, well, still workarounds. You want to force unbehaving functions into something that is unnatural to them:
- In some cases you had to name the parameters,
- in the other you had to use
%$%instead of%>%and where not allowed to use.in your model definition, - if you wanted to use
%>%you had to use alsowithand include.as the second parameter.
The idea of avoiding such “hacks”
motivated me to write intubate.
The intubate alternative
library(intubate)
For Example 1:
No need to specify formula.
LifeCycleSavings %>%
ntbt(lm, sr ~ .)
##
## Call:
## lm(formula = sr ~ ., data = .)
##
## Coefficients:
## (Intercept) pop15 pop75 dpi ddpi
## 28.5660865 -0.4611931 -1.6914977 -0.0003369 0.4096949
or
LifeCycleSavings %>%
ntbt_lm(sr ~ .)
##
## Call:
## lm(formula = sr ~ ., data = .)
##
## Coefficients:
## (Intercept) pop15 pop75 dpi ddpi
## 28.5660865 -0.4611931 -1.6914977 -0.0003369 0.4096949
For Example 2:
No need to specify x.
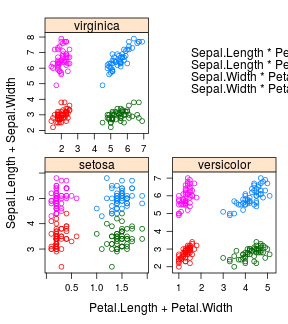
iris %>%
ntbt(xyplot, Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
or
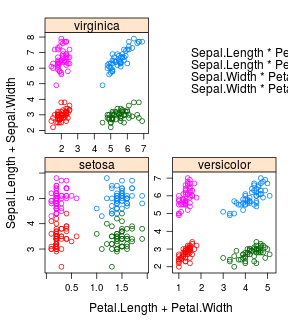
iris %>%
ntbt_xyplot(Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
For Example 3:
No need to specify object.
iris %>%
ntbt(tmd, Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
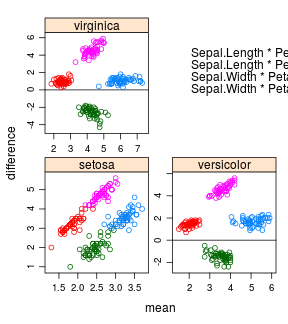
or
iris %>%
ntbt_tmd(Sepal.Length + Sepal.Width ~ Petal.Length + Petal.Width | Species,
scales = "free", layout = c(2, 2),
auto.key = list(x = .6, y = .7, corner = c(0, 0)))
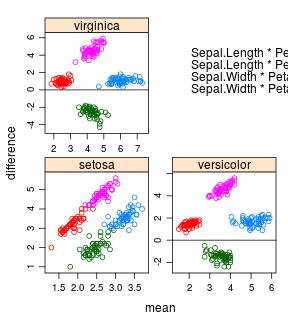
For Example 4:
No need to specify model.
Ovary %>%
ntbt(gls, follicles ~ sin(2*pi*Time) + cos(2*pi*Time),
correlation = corAR1(form = ~ 1 | Mare))
## Generalized least squares fit by REML
## Model: follicles ~ sin(2 * pi * Time) + cos(2 * pi * Time)
## Data: NULL
## Log-restricted-likelihood: -780.7273
##
## Coefficients:
## (Intercept) sin(2 * pi * Time) cos(2 * pi * Time)
## 12.2163982 -2.7747122 -0.8996047
##
## Correlation Structure: AR(1)
## Formula: ~1 | Mare
## Parameter estimate(s):
## Phi
## 0.7532079
## Degrees of freedom: 308 total; 305 residual
## Residual standard error: 4.616172
or
Ovary %>%
ntbt_gls(follicles ~ sin(2*pi*Time) + cos(2*pi*Time),
correlation = corAR1(form = ~ 1 | Mare))
## Generalized least squares fit by REML
## Model: follicles ~ sin(2 * pi * Time) + cos(2 * pi * Time)
## Data: NULL
## Log-restricted-likelihood: -780.7273
##
## Coefficients:
## (Intercept) sin(2 * pi * Time) cos(2 * pi * Time)
## 12.2163982 -2.7747122 -0.8996047
##
## Correlation Structure: AR(1)
## Formula: ~1 | Mare
## Parameter estimate(s):
## Phi
## 0.7532079
## Degrees of freedom: 308 total; 305 residual
## Residual standard error: 4.616172
For Example 5:
No need to specify fixed.
Orthodont %>%
ntbt(lme, distance ~ age)
## Linear mixed-effects model fit by REML
## Data: .
## Log-restricted-likelihood: -221.3183
## Fixed: distance ~ age
## (Intercept) age
## 16.7611111 0.6601852
##
## Random effects:
## Formula: ~age | Subject
## Structure: General positive-definite
## StdDev Corr
## (Intercept) 2.3270339 (Intr)
## age 0.2264276 -0.609
## Residual 1.3100399
##
## Number of Observations: 108
## Number of Groups: 27
or
Orthodont %>%
ntbt_lme(distance ~ age)
## Linear mixed-effects model fit by REML
## Data: .
## Log-restricted-likelihood: -221.3183
## Fixed: distance ~ age
## (Intercept) age
## 16.7611111 0.6601852
##
## Random effects:
## Formula: ~age | Subject
## Structure: General positive-definite
## StdDev Corr
## (Intercept) 2.3270339 (Intr)
## age 0.2264276 -0.609
## Residual 1.3100399
##
## Number of Observations: 108
## Number of Groups: 27
For Example of error 1:
It simply works.
USJudgeRatings %>%
ntbt(cor.test, ~ CONT + INTG)
##
## Pearson's product-moment correlation
##
## data: CONT and INTG
## t = -0.8605, df = 41, p-value = 0.3945
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4168591 0.1741182
## sample estimates:
## cor
## -0.1331909
or
USJudgeRatings %>%
ntbt_cor.test(~ CONT + INTG)
##
## Pearson's product-moment correlation
##
## data: CONT and INTG
## t = -0.8605, df = 41, p-value = 0.3945
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.4168591 0.1741182
## sample estimates:
## cor
## -0.1331909
For Example of error 2:
It simply works.
ToothGrowth %>%
ntbt(aggregate, len ~ ., mean)
## supp dose len
## 1 OJ 0.5 13.23
## 2 VC 0.5 7.98
## 3 OJ 1.0 22.70
## 4 VC 1.0 16.77
## 5 OJ 2.0 26.06
## 6 VC 2.0 26.14
or
ToothGrowth %>%
ntbt_aggregate(len ~ ., mean)
## supp dose len
## 1 OJ 0.5 13.23
## 2 VC 0.5 7.98
## 3 OJ 1.0 22.70
## 4 VC 1.0 16.77
## 5 OJ 2.0 26.06
## 6 VC 2.0 26.14
For Example of error 3:
It simply works.
Iris %>%
ntbt(lda, Sp ~ .)
## Call:
## lda(Sp ~ ., data = .)
##
## Prior probabilities of groups:
## c s v
## 0.3333333 0.3333333 0.3333333
##
## Group means:
## Sepal.L. Sepal.W. Petal.L. Petal.W.
## c 5.936 2.770 4.260 1.326
## s 5.006 3.428 1.462 0.246
## v 6.588 2.974 5.552 2.026
##
## Coefficients of linear discriminants:
## LD1 LD2
## Sepal.L. -0.8293776 0.02410215
## Sepal.W. -1.5344731 2.16452123
## Petal.L. 2.2012117 -0.93192121
## Petal.W. 2.8104603 2.83918785
##
## Proportion of trace:
## LD1 LD2
## 0.9912 0.0088
or
Iris %>%
ntbt_lda(Sp ~ .)
## Call:
## lda(Sp ~ ., data = .)
##
## Prior probabilities of groups:
## c s v
## 0.3333333 0.3333333 0.3333333
##
## Group means:
## Sepal.L. Sepal.W. Petal.L. Petal.W.
## c 5.936 2.770 4.260 1.326
## s 5.006 3.428 1.462 0.246
## v 6.588 2.974 5.552 2.026
##
## Coefficients of linear discriminants:
## LD1 LD2
## Sepal.L. -0.8293776 0.02410215
## Sepal.W. -1.5344731 2.16452123
## Petal.L. 2.2012117 -0.93192121
## Petal.W. 2.8104603 2.83918785
##
## Proportion of trace:
## LD1 LD2
## 0.9912 0.0088
I think the approach intubate proposes
looks consistent, elegant, simple and clean,
less error prone, and easy to follow (of course,
keep in mind that I have a vested interest in the
success of intubate).
After all, the complication should be in the analysis you are performing, and not in how you are performing it.